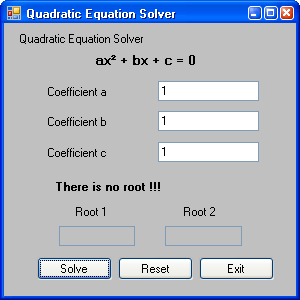
Quadratic Equation Solver is a small application which allows you to solve a quadratic equation and produce the result very fast and correct.
Here is the source code of the application "Quadratic Equation Solver"
Code :
Module Module1
Public a, b, c, det, r1, r2 As Single
End Module
Imports System.Console
Imports System.Math
Public Class Form1
Private Sub Form1_Load(ByVal sender As System.Object, ByVal e As System.EventArgs) HandlesMyBase.Load
Texta.Text = ""
Textb.Text = ""
Textc.Text = ""
Textr1.Text = ""
Textr2.Text = ""
End Sub
Private Sub Button4_Click(ByVal sender As System.Object, ByVal e As System.EventArgs)Handles QESExit.Click
End
End Sub
Private Sub Solve_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) HandlesSolve.Click
Textr1.Text = ""
Textr2.Text = ""
If Texta.Text = "0" Then
MsgBox("Cofficient a must not be 0 !!!")
Texta.Text = ""
Texta.Focus()
ElseIf Texta.Text = "" Or IsNothing(Texta.Text) Or IsNumeric(Texta.Text) = False Then
MsgBox("Cofficient a must have an numberic value !!!")
Texta.Text = ""
Texta.Focus()
ElseIf Textb.Text = "" Or IsNothing(Textb.Text) Or IsNumeric(Textb.Text) = False Then
MsgBox("Cofficient b must have an numberic value !!!")
Textb.Text = ""
Textb.Focus()
ElseIf Textc.Text = "" Or IsNothing(Textc.Text) Or IsNumeric(Textc.Text) = False Then
MsgBox("Cofficient a must have an numberic value !!!")
Textc.Text = ""
Textc.Focus()
Else
a = Texta.Text
b = Textb.Text
c = Textc.Text
det = (b * b) - (4 * a * c)
If (det > 0) Then
r1 = (-b + Sqrt(det)) / (2 * a)
r2 = (-b - Sqrt(det)) / (2 * a)
Answer.Text = "There are two roots :: "
Textr1.Enabled = True
Textr2.Enabled = True
Textr1.Text = r1
Textr2.Text = r2
ElseIf (det = 0) Then
r1 = (-b + Sqrt(det)) / (2 * a)
Answer.Text = "There is only one root :: "
Textr1.Enabled = True
Textr1.Text = r1
Else
Answer.Text = "There is no root !!!"
End If
End If
End Sub
Private Sub Reset_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) HandlesReset.Click
Texta.Text = ""
Textb.Text = ""
Textc.Text = ""
Textr1.Text = ""
Textr2.Text = ""
Answer.Text = ""
Textr1.Enabled = False
Textr2.Enabled = False
Texta.Focus()
End Sub
Private Sub Texta_GotFocus(ByVal sender As Object, ByVal e As System.EventArgs) HandlesTexta.GotFocus
Texta.SelectAll()
End Sub
Private Sub Textb_GotFocus(ByVal sender As Object, ByVal e As System.EventArgs) HandlesTextb.GotFocus
Textb.SelectAll()
End Sub
Private Sub Textc_GotFocus(ByVal sender As Object, ByVal e As System.EventArgs) HandlesTextc.GotFocus
Textc.SelectAll()
End Sub
End Class
Output :
This is the simple view of the application
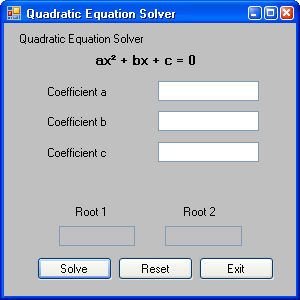
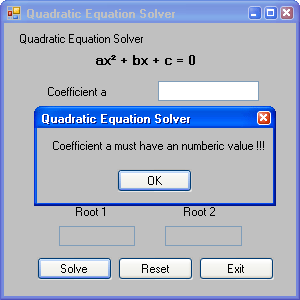
When you leave any text box as blank you will see an message box as shown in below figure
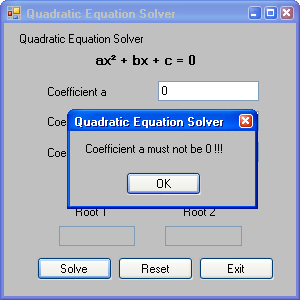
When you assign a 0 to "coefficient a" You will receive an message box as shown in below figure
Solution in case of two roots found
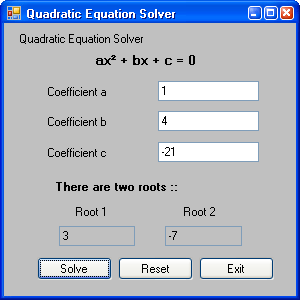
Solution in case of one root found
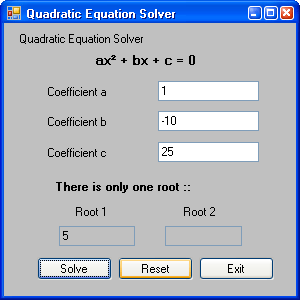
Solution in case of no root found